Equações de 2º grau
Definições
Denomina-se equação do 2º grau na incógnita x, toda equação da forma:
ax2 + bx + c = 0; a, b, c
|
Exemplo:
- x2 - 5x + 6 = 0 é um equação do 2º grau com a = 1, b = -5 e c = 6.
- 6x2 - x - 1 = 0 é um equação do 2º grau com a = 6, b = -1 e c = -1.
- 7x2 - x = 0 é um equação do 2º grau com a = 7, b = -1 e c = 0.
- x2 - 36 = 0 é um equação do 2º grau com a = 1, b = 0 e c = -36.
Nas equações escritas na forma ax² + bx + c = 0 (forma normal ou forma reduzida de uma equação do 2º grau na incógnita x) chamamos a, b e c de coeficientes.
a é sempre o coeficiente de x²;
b é sempre o coeficiente de x,
c é o coeficiente ou termo independente.
Equação completas e Incompletas
Uma equação do 2º grau é completa quando b e c são diferentes de zero. Exemplos:
x² - 9x + 20 = 0 e -x² + 10x - 16 = 0 são equações completas.
Uma equação do 2º grau é incompleta quando b ou c é igual a zero, ou ainda quando ambos são iguais a zero. Exemplos:
|
|
|
| Resolução de equações incompletas Resolver uma equação significa determinar o seu conjunto verdade. Utilizamos na resolução de uma equação incompleta as técnicas da fatoração e duas importantes propriedades dos números reais: 1ª Propriedade: 2ª Propriedade: 1º Caso: Equação do tipo Exemplo:
Para o produto ser igual a zero, basta que um dos fatores também o seja. Assim:
Obtemos dessa maneira duas raízes que formam o conjunto verdade:
De modo geral, a equação do tipo
2º Caso: Equação do tipo
Exemplos:
Solução

De modo geral, a equação do tipo
|
Resolução de equações completas
Para solucionar equações completas do 2º grau utilizaremos a fórmula de Bhaskara.
A partir da equação
1º passo: multiplicaremos ambos os membros por 4a.
|
2º passo: passar 4ac par o 2º membro.
|
3º passo: adicionar
|
4º passo: fatorar o 1º elemento.
|
5º passo: extrair a raiz quadrada dois membros.
|
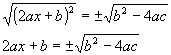
6º passo: passar b para o 2º membro.
|
7º passo: dividir os dois membros por
|
Assim, encontramos a fórmula resolutiva da equação do 2º grau:
Podemos representar as duas raízes reais por x' e x", assim:
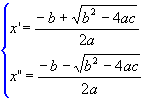
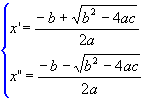
Exemplos:
- resolução a equação:
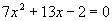
Temos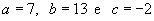
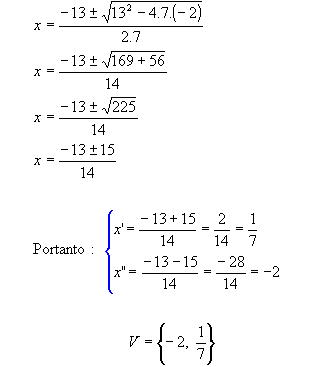
FONTE: SóMatemática
ATIVIDADES
- Exercícios online 1
- Exercícios online 2
- Exercícios online 3
- Exercícios online 4
- Exercícios online 5
- Exercícios online 6
- Exercícios online 7
- Exercícios online 8
- Exercícios online 9
- Exercícios online 10
- Exercícios online 11
- Exercícios online 12
- Jogo 1
- Jogo 2
- Jogo 3: Fase 1 - Fase 2 - Fase 3 - Fase 4
- Jogo 4
- Jogo 5

Nenhum comentário:
Postar um comentário
Mande sua mensagem, mas cuidado, ofensas de qualquer tipo NÂO serão publicadas. Obrigada.