Atividade 1
sexta-feira, 30 de novembro de 2018
Educação Infantil -
1. Formas Geométricas
2. Memória Animal
Atividade 3
Atividade 4: O que está fora do lugar?
quarta-feira, 21 de novembro de 2018
terça-feira, 20 de novembro de 2018
FUNÇÃO DE 2º GRAU
FUNÇÕES DE 2º GRAU
Chama-se função quadrática, ou função polinomial do 2º grau, qualquer função f de IR em IR dada por uma lei da forma f(x) = ax2 + bx + c, onde a, b e c são números reais e a  0. Vejamos alguns exemplos de funções quadráticas:
0. Vejamos alguns exemplos de funções quadráticas:
- f(x) = 3x2 - 4x + 1, onde a = 3, b = - 4 e c = 1
- f(x) = x2 -1, onde a = 1, b = 0 e c = -1
- f(x) = 2x2 + 3x + 5, onde a = 2, b = 3 e c = 5
- f(x) = - x2 + 8x, onde a = -1, b = 8 e c = 0
- f(x) = -4x2, onde a = - 4, b = 0 e c = 0
Gráfico
O gráfico de uma função polinomial do 2º grau, y = ax2 + bx + c, com a  0, é uma curva chamada parábola.
0, é uma curva chamada parábola.
 0, é uma curva chamada parábola.
0, é uma curva chamada parábola.
Por exemplo, vamos construir o gráfico da função y = x2 + x:
Primeiro atribuímos a x alguns valores, depois calculamos o valor correspondente de y e, em seguida, ligamos os pontos assim obtidos.
| x | y |
| -3 | 6 |
| -2 | 2 |
| -1 | 0 |
| 0 | 0 |
| 1 | 2 |
| 2 | 6 |
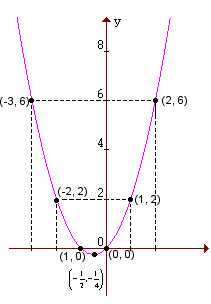
Observação:
Ao construir o gráfico de uma função quadrática y = ax2 + bx + c, notaremos sempre que:
- se a > 0, a parábola tem a concavidade voltada para cima;
- se a < 0, a parábola tem a concavidade voltada para baixo;
Zeros ou raízes da função de 2º Grau
Chamam-se zeros ou raízes da função polinomial do 2º grau f(x) = ax2 + bx + c , a  0, os números reais x tais que f(x) = 0.
0, os números reais x tais que f(x) = 0.
 0, os números reais x tais que f(x) = 0.
0, os números reais x tais que f(x) = 0.
Então as raízes da função f(x) = ax2 + bx + c são as soluções da equação do 2º grau ax2 + bx + c = 0, as quais são dadas pela chamada fórmula de Bhaskara:
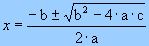 |
Temos:
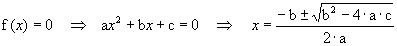
Observação:
A quantidade de raízes reais de uma função quadrática depende do valor obtido para o
radicando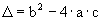 , chamado discriminante, a saber:
, chamado discriminante, a saber:
radicando
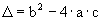 , chamado discriminante, a saber:
, chamado discriminante, a saber:- quando
 é positivo, há duas raízes reais e distintas;
é positivo, há duas raízes reais e distintas;
- quando
 é zero, há só uma raiz real (para ser mais preciso, há duas raízes iguais);
é zero, há só uma raiz real (para ser mais preciso, há duas raízes iguais);
- quando
 é negativo, não há raiz real.
é negativo, não há raiz real.
Coordenadas do vértice da parábola
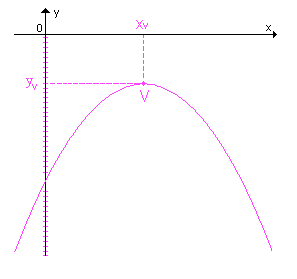
Quando a > 0, a parábola tem concavidade voltada para cima e um ponto de mínimo V; quando a < 0, a parábola tem concavidade voltada para baixo e um ponto de máximo V.
Em qualquer caso, as coordenadas de V são 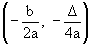 . Veja os gráficos:
. Veja os gráficos:
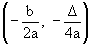 . Veja os gráficos:
. Veja os gráficos: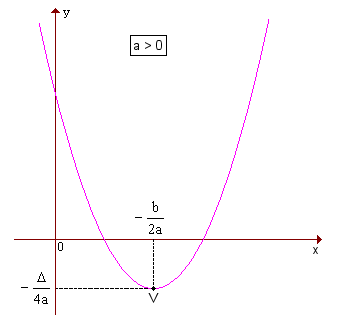
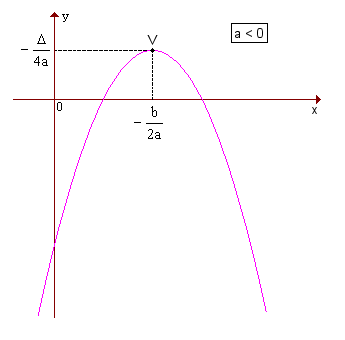
Imagem
O conjunto-imagem Im da função y = ax2 + bx + c, a  0, é o conjunto dos valores que y pode assumir. Há duas possibilidades:
0, é o conjunto dos valores que y pode assumir. Há duas possibilidades:
 0, é o conjunto dos valores que y pode assumir. Há duas possibilidades:
0, é o conjunto dos valores que y pode assumir. Há duas possibilidades:
1ª - quando a > 0,
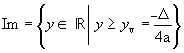
a > 0
|
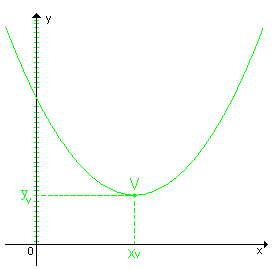
2ª quando a < 0,
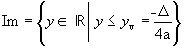
a < 0
|
Construção da parábola
É possível construir o gráfico de uma função do 2º grau sem montar a tabela de pares (x, y), mas seguindo apenas o roteiro de observação seguinte:
- O valor do coeficiente a define a concavidade da parábola;
- Os zeros definem os pontos em que a parábola intercepta o eixo dos x;
- O vértice V
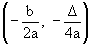 indica o ponto de mínimo (se a > 0), ou máximo (se a< 0);
indica o ponto de mínimo (se a > 0), ou máximo (se a< 0); - A reta que passa por V e é paralela ao eixo dos y é o eixo de simetria da parábola;
- Para x=0 , temos y = a·02 + b·0 + c = c; então (0, c) é o ponto em que a parábola corta o eixo dos y.
Gerador de Gráficos: Função de Segundo Grau
 |
| http://odin.mat.ufrgs.br/outros/fernando/cri_ger_2g/index.php |
Usando o gerador e mais o que você sabe, resolva os exercícios abaixo:
- https://www.tutorbrasil.com.br/aulas-de-matematica/funcoes-2-grau/exercicios-funcao-2-grau/
- http://blog.educacaoadventista.org.br/maticaceama/arquivos/9-ano-funcoes-do-2-grau-equacoes-biquadradas-equacoes-irracionais.pdf
- http://www.colegioequipe.com.br/muriae/wp-content/uploads/sites/5/2%C2%AA-ATIVIDADE-EXTRA-9%C2%BA-ANO-TESTE-28.pdf
Agora que você está craque, vamos fazer o teste da Khan Academy?
 |
| https://pt.khanacademy.org/math/algebra-home/alg-functions#alg-functions-unit-test |
Assinar:
Comentários (Atom)
















